MEKANIKA KUANTUM
Mekanika klasik meskipun sukses menganalisis dinamika benda makroskopik, ternyata tidak akurat menangani dinamika benda mikroskopik seperti atom. Pengertian mikroskopik dalam skala atomik bersifat mutlak. Sistem dikategorikan mikroskopik jika fenomenanya tidak lagi dapat dijelaskan oleh mekanika klasik.
Pengamatan dalam ranah mekanika klasik tidak mengganggu keadaan sistem. Hal ini berbeda dengan pengamatan dalam ranah mekanika kuantum, sebab pengamatan berarti mengganggu keadaan sistem. Contohnya adalah aplikasi persamaan Maxwell, dimana diasumsikan bahwa arus dan medan listrik indexmedan!listrik dapat diukur secara bersamaan tanpa masalah, tidak terjadi perubahan nilai akibat urutan pengamatan. Menurut mekanika klasik, ketidak pastian pengukuran dapat dikoreksi, misalnya dengan melakukan pengamatan berkali-kali atau dengan menggunakan alat ukur yang lebih akurat.
Pengamatan paling lumrah dalam ranah kuantum adalah dengan menjatuhkan cahaya pada benda. Dalam skala mikro, menjatuhkan cahaya pada benda berarti membombardirnya dengan foton. Jika pengamatan dimaksudkan untuk menentukan posisi secara akurat, maka panjang gelombang cahaya yang digunakan harus cukup kecil, yang berarti frekuensinya cukup besar. Jika energi cukup besar maka melakukan pengamatan terhadap sistem kecil berarti mengganggu sistem tersebut. Sebab itu akurasi pengamatan memiliki keterbatasan. Keterbatasan ini tidak mungkin dihilangkan dengan memperbaiki teknik pengamatan (pengukuran). Dalam upaya memahami akibat gangguan terhadap sistem dan respon sistem terhadap gangguan, kita memerlukan teori baru, yakni mekanika kuantum.
Uraian di atas menunjukkan bahwa fisika kuantum cukup rumit sebab menyangkut perumusan teori informasi, sedangkan informasinya diperoleh dengan cara yang tampak janggal. Kendati demikian, cukup mencengangkan sebab ternyata teori kuantum cukup rapi dan akurat dalam menjelaskan gejala yang tidak lagi dapat dijelaskan secara klasik.
Point pertama dari mekanika kuantum adalah pengaruh yang ditimbulkan oleh pengamatan terhadap sistem; pengaruh ini tentu muncul secara eksplisit dalam teori. Terdapat 2 sifat utama pengamatan
- Untuk setiap pengukuran besaran fisis (energi, momentum dan posisi) terdapat himpunan bilangan yang bersesuaian dengan semua hasil yang mungkin dari pengukuran bersangkutan. Bilangan-bilangan itu dapat bernilai kontinu atau diskret, misalnya spektrum energi atom hidrogen.
- Jika terdapat dua jenis pengukuran, yaitu pengukuran A dan B; misalkan A untuk posisi, dan B untuk momentum, maka hasil pengukuran dipengaruhi oleh urutan pengukuran. Urutan pengukuran A yang diikuti oleh B dan disimbolkan sebagai pada umumnya berbeda hasilnya dengan urutan pengukuran
 . Penyebabnya adalah karena masing-masing pengukuran dapat mengganggu keadaan sistem. Kenyataan ini secara umum disimbolkan sebagai
. Penyebabnya adalah karena masing-masing pengukuran dapat mengganggu keadaan sistem. Kenyataan ini secara umum disimbolkan sebagai
Mekanika kuantum adalah cabang dasar fisika yang menggantikan mekanika klasik pada tataran atom dan subatom. Ilmu ini memberikan kerangka matematika untuk berbagai cabang fisika dan kimia, termasuk fisika atom, fisika molekular, kimia komputasi, kimia kuantum, fisika partikel, dan fisika nuklir. Mekanika kuantum adalah bagian dari teori medan kuantum dan fisika kuantum umumnya, yang, bersama relativitas umum, merupakan salah satu pilar fisika modern. Dasar dari mekanika kuantum adalah bahwa energi itu tidak kontinyu, tapi diskrit -- berupa 'paket' atau 'kuanta'. Konsep ini cukup revolusioner, karena bertentangan dengan fisika klasik yang berasumsi bahwa energi itu berkesinambungan.
Sejarah
Niels Bohr (1885-1962): Pioner mekanika kuantum
 Teori struktur atom mempunyai seorang bapak. Dia itu Niels Henrik David Bohr yang lahir tahun 1885 di Kopenhagen. Di tahun 1911 dia raih gelar doktor fisika dari Universitas Copenhagen. Tak lama sesudah itu dia pergi ke Cambridge, Inggris. Di situ dia belajar di bawah asuhan J.J. Thompson, ilmuwan kenamaan yang menemukan elektron. Hanya dalam beberapa bulan sesudah itu Bohr pindah lagi ke Manchester, belajar pada Ernest Rutherford yang beberapa tahun sebelumnya menemukan nucleus (bagian inti) atom. Adalah Rutherford ini yang menegaskan (berbeda dengan pendapat-pendapat sebelumnya) bahwa atom umumnya kosong, dengan bagian pokok yang berat pada tengahnya dan elektron di bagian luarnya. Tak lama sesudah itu Bohr segera mengembangkan teorinya sendiri yang baru serta radikal tentang struktur atom.
Teori struktur atom mempunyai seorang bapak. Dia itu Niels Henrik David Bohr yang lahir tahun 1885 di Kopenhagen. Di tahun 1911 dia raih gelar doktor fisika dari Universitas Copenhagen. Tak lama sesudah itu dia pergi ke Cambridge, Inggris. Di situ dia belajar di bawah asuhan J.J. Thompson, ilmuwan kenamaan yang menemukan elektron. Hanya dalam beberapa bulan sesudah itu Bohr pindah lagi ke Manchester, belajar pada Ernest Rutherford yang beberapa tahun sebelumnya menemukan nucleus (bagian inti) atom. Adalah Rutherford ini yang menegaskan (berbeda dengan pendapat-pendapat sebelumnya) bahwa atom umumnya kosong, dengan bagian pokok yang berat pada tengahnya dan elektron di bagian luarnya. Tak lama sesudah itu Bohr segera mengembangkan teorinya sendiri yang baru serta radikal tentang struktur atom.
Kertas kerja Bohr yang bagaikan membuai sejarah "On the Constitution of Atoms and Molecules," diterbitkan dalam Philosophical Magazine tahun 1933.
Teori Bohr memperkenalkan atom sebagai sejenis miniatur planit mengitari matahari, dengan elektron-elektron mengelilingi orbitnya sekitar bagian pokok, tetapi dengan perbedaan yang sangat penting: bilamana hukum-hukum fisika klasik mengatakan tentang perputaran orbit dalam segala ukuran, Bohr membuktikan bahwa elektron-elektron dalam sebuah atom hanya dapat berputar dalam orbitnya dalam ukuran spesifik tertentu. Atau dalam kalimat rumusan lain: elektron-elektron yang mengitari bagian pokok berada pada tingkat energi (kulit) tertentu tanpa menyerap atau memancarkan energi. Elektron dapat berpindah dari lapisan dalam ke lapisan luar jika menyerap energi. Sebaliknya, elektron akan berpindah dari lapisan luar ke lapisan lebih dalam dengan memancarkan energi.
Teori Bohr memperkenalkan perbedaan radikal dengan gagasan teori klasik fisika. Beberapa ilmuwan yang penuh imajinasi (seperti Einstein) segera bergegas memuji kertas kerja Bohr sebagai suatu "masterpiece," suatu kerja besar; meski begitu, banyak ilmuwan lainnya pada mulanya menganggap sepi kebenaran teori baru ini. Percobaan yang paling kritis adalah kemampuan teori Bohr menjelaskan spektrum dari hydrogen atom. Telah lama diketahui bahwa gas hydrogen jika dipanaskan pada tingkat kepanasan tinggi, akan mengeluarkan cahaya. Tetapi, cahaya ini tidaklah mencakup semua warna, tetapi hanya cahaya dari sesuatu frekuensi tertentu. Nilai terbesar dari teori Bohr tentang atom adalah berangkat dari hipotesa sederhana tetapi sanggup menjelaskan dengan ketetapan yang mengagumkan tentang gelombang panjang yang persis dari semua garis spektral (warna) yang dikeluarkan oleh hidrogen. Lebih jauh dari itu, teori Bohr memperkirakan adanya garis spektral tambahan, tidak terlihat pada saat sebelumnya, tetapi kemudian dipastikan oleh para pencoba. Sebagai tambahan, teori Bohr tentang struktur atom menyuguhkan penjelasan pertama yang jelas apa sebab atom punya ukuran seperti adanya. Ditilik dari semua kejadian yang meyakinkan ini, teori Bohr segera diterima, dan di tahun 1922 Bohr dapat,hadiah Nobel untuk bidang fisika.
Tahun 1920 lembaga Fisika Teoritis didirikan di Kopenhagen dan Bohr jadi direkturnya. Di bawah pirnpinannya cepat menarik minat ilmuwan-ilmuwan muda yang brilian dan segera menjadi pusat penyelidikan ilmiah dunia.
Tetapi sementara itu teori struktur atom Bohr menghadapi kesulitan-kesulitan. Masalah terpokok adalah bahwa teori Bohr, meskipun dengan sempurna menjelaskan kesulitan masa depan atom (misalnya hidrogen) yang punya satu elektron, tidak dengan persis memperkirakan spektra dari atom-atom lain. Beberapa ilmuwan, terpukau oleh sukses luar biasa teori Bohr dalam hal memaparkan atom hidrogen, berharap dengan jalan menyempurnakan sedikit teori Bohr, mereka dapat juga menjelaskan spektra atom yang lebih berat. Bohr sendiri merupakan salah seorang pertama yang menyadari penyempurnaan kecil itu tak akan menolong, karena itu yang diperlukan adalah perombakan radikal. Tetapi, bagaimanapun dia mengerahkan segenap akal geniusnya, toh dia tidak mampu memecahkannya.
Pemecahan akhirnya ditemukan oleh Werner Heisenberg dan lain-lainnya, mulai tahun 1925. Adalah menarik untuk dicatat di sini, bahwa Heisenberg –dan umumnya ilmuwan yang mengembangkan teori baru– belajar di Kopenhagen, yang tak syak lagi telah mengambil manfaat yang besar dari diskusi-diskusi dengan Bohr dan saling berhubungan satu sama lain. Bohr sendiri bergegas menuju ide baru itu dan membantu mengembangkannya. Dia membuat sumbangan penting terhadap teori baru, dan liwat disuksi-diskusi dan tulisan-tulisan, dia menolong membikin lebih sistematis.
Tahun 1930-an lebih menunjukkan perhatiannya terhadap permasalahan bagian pokok struktur atom. Dia mengembangkan model penting "tetesan cairan" bagian pokok atom. Dia juga mengajukan masalah teori tentang "kombinasi bagian pokok" dalam reaksi atom untuk dipecahkan. Tambahan pula, Bohr merupakan orang yang dengan cepat menyatakan bahwa isotop uranium yang terlibat dalam pembagian nuklir adalah U235. Pernyataan ini punya makna penting dalam pengembangan berikutnya dari bom atom.
Dalam tahun 1940 balatentara Jerman menduduki Denmark. Ini menempatkan diri Bohr dalam bahaya, sebagian karena dia punya sikap anti Nazi sudah tersebar luas, sebagian karena ibunya seorang Yahudi. Tahun 1943 Bohr lari meninggalkan Denmark yang jadi daerah pendudukan, menuju Swedia. Dia juga menolong sejumlah besar orang Yahudi Denmark melarikan diri agar terhindar dari kematian dalam kamar-kamar gas Hitler. Dari Swedia Bohr lari ke Inggris dan dari sana menyeberang ke Amerika Serikat. Di negeri ini, selama perang berlangsung, Bohr membantu membikin bom atom,
Seusai perang, Bohr kembali kampung ke Denmark dan mengepalai lembaga hingga rohnya melayang tahun 1`562. Dalam tahun-tahun sesudah perang Bohr berusaha keras –walau tak berhasil– mendorong dunia internasional agar mengawasi penggunaan energi atom.
Bohr kawin tahun 1912, di sekitar saat-saat dia melakukan kerja besar di bidang ilmu pengetahuan. Dia punya lima anak, salah seorang bernama Aage Bohr, memenangkan hadiah Nobel untuk bidang fisika di tahun 1975. Bohr merupakan orang yang paling disenangi di dunia ilmuwan, bukan semata-mata karena menghormat ilmunya yang genius, tetapi juga pribadinya dan karakter serta rasa kemanusiaannya yang mendalam.
Kendati teori orisinal Bohr tentang struktur atom sudah berlalu lima puluh tahun yang lampau, dia tetap merupakan salah satu dari tokoh besar di abad ke-20. Ada beberapa alasan mengapa begitu. Pertama, sebagian dari hal-hal penting teorinya masih tetap dianggap benar. Misalnya, gagasannya bahwa atom dapat ada hanya pada tingkat energi yang cermat adalah merupakan bagian tak terpisahkan dari semua teori-teori struktur atom berikutnya. Hal lainnya lagi, gambaran Bohr tentang atom punya arti besar buat menemukan sesuatu untuk diri sendiri, meskipun ilmuwan modern tak menganggap hal itu secara harfiah benar. Yang paling penting dari semuanya itu, mungkin, adalah gagasan Bohr yang merupakan tenaga pendorong bagi perkembangan "teori kuantum." Meskipun beberapa gagasannya telah kedaluwarsa, namun jelas secara historis teori-teorinya sudah membuktikan merupakan titik tolak teori modern tentang atom dan perkembangan berikutnya bidang mekanika kuantum.
Pada tahun 1900, Max Planck memperkenalkan ide bahwa energi dapat dibagi-bagi menjadi beberapa paket atau kuanta. Ide ini secara khusus digunakan untuk menjelaskan sebaran intensitas radiasi yang dipancarkan oleh benda hitam. Pada tahun 1905, Albert Einstein menjelaskan efek fotoelektrik dengan menyimpulkan bahwa energi cahaya datang dalam bentuk kuanta yang disebut foton. Pada tahun 1913, Niels Bohr menjelaskan garis spektrum dari atom hidrogen, lagi dengan menggunakan kuantisasi. Pada tahun 1924, Louis de Broglie memberikan teorinya tentang gelombang benda.
Teori-teori di atas, meskipun sukses, tetapi sangat fenomenologikal: tidak ada penjelasan jelas untuk kuantisasi. Mereka dikenal sebagai teori kuantum lama.
Frase "Fisika kuantum" pertama kali digunakan oleh Johnston dalam tulisannya Planck's Universe in Light of Modern Physics (Alam Planck dalam cahaya Fisika Modern).
Mekanika kuantum modern lahir pada tahun 1925, ketika Werner Karl Heisenberg mengembangkan mekanika matriks dan Erwin Schrödinger menemukan mekanika gelombang dan persamaan Schrödinger. Schrödinger beberapa kali menunjukkan bahwa kedua pendekatan tersebut sama.
Heisenberg merumuskan prinsip ketidakpastiannya pada tahun 1927, dan interpretasi Kopenhagen terbentuk dalam waktu yang hampir bersamaan. Pada 1927, Paul Dirac menggabungkan mekanika kuantum dengan relativitas khusus. Dia juga membuka penggunaan teori operator, termasuk notasi bra-ket yang berpengaruh. Pada tahun 1932, Neumann Janos merumuskan dasar matematika yang kuat untuk mekanika kuantum sebagai teori operator.
Bidang kimia kuantum dibuka oleh Walter Heitler dan Fritz London, yang mempublikasikan penelitian ikatan kovalen dari molekul hidrogen pada tahun 1927. Kimia kuantum beberapa kali dikembangkan oleh pekerja dalam jumlah besar, termasuk kimiawan Amerika Linus Pauling.
Berawal pada 1927, percobaan dimulai untuk menggunakan mekanika kuantum ke dalam bidang di luar partikel satuan, yang menghasilkan teori medan kuantum. Pekerja awal dalam bidang ini termasuk Dirac, Wolfgang Pauli, Victor Weisskopf dan Pascaul Jordan. Bidang riset area ini dikembangkan dalam formulasi elektrodinamika kuantum oleh Richard Feynman, Freeman Dyson, Julian Schwinger, dan Tomonaga Shin'ichirō pada tahun 1940-an. Elektrodinamika kuantum adalah teori kuantum elektron, positron, dan Medan elektromagnetik, dan berlaku sebagai contoh untuk teori kuantum berikutnya.
Interpretasi banyak dunia diformulasikan oleh Hugh Everett pada tahun 1956.
Teori Kromodinamika kuantum diformulasikan pada awal 1960an. Teori yang kita kenal sekarang ini diformulasikan oleh Polizter, Gross and Wilzcek pada tahun 1975. Pengembangan awal oleh Schwinger, Peter Higgs, Goldstone dan lain-lain. Sheldon Lee Glashow, Steven Weinberg dan Abdus Salam menunjukan secara independen bagaimana gaya nuklir lemah dan elektrodinamika kuantum dapat digabungkan menjadi satu gaya lemah elektro.
Kelahiran mekanika kuantum
a. Sifat gelombang partikel
Di paruh pertama abad 20, mulai diketahui bahwa gelombang elektromagnetik, yang sebelumnya dianggap gelombang murni, berperilaku seperti partikel (foton). Fisikawan Perancis Louis Victor De Broglie (1892-1987) mengasumsikan bahwa sebaliknya mungkin juga benar, yakni materi juga berperilaku seperti gelombang. Berawal dari persamaan Einstein, E = cp dengan p adalah momentum foton, c kecepatan cahaya dan E adalah energi, ia mendapatkan hubungan:
E = hν =ν = c/λ atau hc/ λ = E, maka h/ λ= p … (2.12)
De Broglie menganggap setiap partikel dengan momentum p = mv disertai dengan gelombang (gelombang materi) dengan panjang gelombang λ didefinisikan dalam persamaan (2.12) (1924). Tabel 2.2 memberikan beberapa contoh panjag gelombang materi yang dihitung dengan persamaan (2.12). Dengan meningkatnya ukuran partikel, panjang gelombangnya menjadi lebih pendek. Jadi untuk partikel makroskopik, particles, tidak dimungkinkan mengamati difraksi dan fenomena lain yang berkaitan dengan gelombang. Untuk partikel mikroskopik, seperti elektron, panjang gelombang materi dapat diamati. Faktanya, pola difraksi elektron diamati (1927) dan membuktikan teori De Broglie.
Tabel 2.2 Panjang-gelombang gelombang materi.
| partikel | massa (g) | kecepatan (cm s-1) | Panjang gelombang (nm) |
| elektron (300K) | 9,1×10-28 | 1,2×107 | 6,1 |
| elektron at 1 V | 9,1×10-28 | 5,9×107 | 0,12 |
| elektron at 100 V | 9,1×10-28 | 5,9×108 | 0,12 |
| He atom 300K | 6,6×10-24 | 1,4×105 | 0,071 |
| Xe atom 300K | 2,2×10-22 | 2,4×104 | 0,012 |
Latihan 2.7 Panjang-gelombang gelombang materi.
Peluru bermassa 2 g bergerak dengan kecepatan 3 x 102 m s-1. Hitung panjang gelombang materi yang berkaitan dengan peluru ini.
Jawab: Dengan menggunakan (2.12) dan 1 J = 1 m2 kg s-2, λ = h/ mv = 6,626 x 10-34 (J s)/ [2,0 x 10-3(kg) x 3 x102(m s-1)] = 1,10 x 10-30 (m2 kg s-1)/ (kg m s-1) = 1,10 x 10-30 m
Perhatikan bahwa panjang gelombang materi yang berkaitan dengan gelombang peluru jauh lebih pendek dari gelombang sinar-X atau γ dan dengan demikian tidak teramati.
b. Prinsip ketidakpastian
Dari yang telah dipelajari tentang gelombang materi, kita dapat mengamati bahwa kehati-hatian harus diberikan bila teori dunia makroskopik akan diterapkan di dunia mikroskopik. Fisikawan Jerman Werner Karl Heisenberg (1901-1976) menyatakan tidak mungkin menentukan secara akurat posisi dan momentum secara simultan partikel yang sangat kecil semacam elektron. Untuk mengamati partikel, seseorang harus meradiasi partikel dengan cahaya. Tumbukan antara partikel dengan foton akan mengubah posisi dan momentum partikel.
Heisenberg menjelaskan bahwa hasil kali antara ketidakpastian posisi ![]() x dan ketidakpastian momentum
x dan ketidakpastian momentum ![]() p akan bernilai sekitar konstanta Planck:
p akan bernilai sekitar konstanta Planck:
![]() x
x![]() p = h (2.13)
p = h (2.13)
Hubungan ini disebut dengan prinsip ketidakpastian Heisenberg.
Latihan 2.8 Ketidakpastian posisi elektron.
Anggap anda ingin menentukan posisi elektron sampai nilai sekitar 5 x 10-12 m. Perkirakan ketidakpastian kecepatan pada kondisi ini.
Jawab: Ketidakpastian momentum diperkirakan dengan persamaan (2.13). ![]() p = h/
p = h/![]() x = 6,626 x 10-34 (J s)/5 x 10-12 (m) = 1,33 x 10-22 (J s m-1). Karena massa elektron 9,1065 x 10-31 kg, ketidakpastian kecepatannya
x = 6,626 x 10-34 (J s)/5 x 10-12 (m) = 1,33 x 10-22 (J s m-1). Karena massa elektron 9,1065 x 10-31 kg, ketidakpastian kecepatannya ![]() v akan benilai:
v akan benilai: ![]() v = 1,33 x 10-22(J s m-1) / 9,10938 x 10-31 (kg) = 1,46 x 108 (m s-1).
v = 1,33 x 10-22(J s m-1) / 9,10938 x 10-31 (kg) = 1,46 x 108 (m s-1).
Perkiraan ketidakpastian kecepatannya hampir setengah kecepatan cahaya (2,998 x108 m s-1) mengindikasikan bahwa jelas tidak mungkin menentukan dengan tepat posisi elektron. Jadi menggambarkan orbit melingkar untuk elektron jelas tidak mungkin.
c. Persamaan Schrödinger
Fisikawan Austria Erwin Schrödinger (1887-1961) mengusulkan ide bahwa persamaan De Broglie dapat diterapkan tidak hanya untuk gerakan bebas partikel, tetapi juga pada gerakan yang terikat seperti elektron dalam atom. Dengan memperuas ide ini, ia merumuskan sistem mekanika gelombang. Pada saat yang sama Heisenberg mengembangkan sistem mekanika matriks. Kemudian hari kedua sistem ini disatukan dalam mekanika kuantum.
Dalam mekanika kuantum, keadaan sistem dideskripsikan dengan fungsi gelombang. Schrödinger mendasarkan teorinya pada ide bahwa energi total sistem, E dapat diperkirakan dengan menyelesaikan persamaan. Karena persamaan ini memiliki kemiripan dengan persamaan yang mengungkapkan gelombang di fisika klasik, maka persamaan ini disebut dengan persamaan gelombang Schrödinger.
Persamaan gelombang partikel (misalnya elektron) yang bergerak dalam satu arah (misalnya arah x) diberikan oleh:
(-h2/8π2m)(d2Ψ/dx2) + VΨ = EΨ … (2.14)
m adalah massa elektron, V adalah energi potensial sistem sebagai fungsi koordinat, dan Ψ adalah fungsi gelombang.
ATOM MIRIP HIDROGEN
Dimungkinkan uintuk memperluas metoda yang digunakan dalam potensial kotak satu dimensi ini untuk menangani atom hidrogen dan atom mirip hidrogen secara umum. Untuk keperluan ini persamaan satu dimensi (2.14) harus diperluas menjadi persamaan tiga dimensi sebagai berikut:
(-h2/8π2m)Ψï¼»(∂2/∂x2) + (∂2/∂y2) +(∂2/∂z2)ï¼½+V(x, y, z)Ψ = EΨ … (2.19)
Bila didefinisikan ∇2 sebagai:
(∂2/∂x2) + (∂2/∂y2) +(∂2/∂z2) = ∇2 … (2.20)
Maka persamaan Schrödinger tiga dimensi akan menjadi:
(-h2/8π2m)∇2Ψ +VΨ = EΨ … (2.21)
atau ∇2Ψ +(8π 2m/h2)(E -V)Ψ = 0 … (2.22)
Energi potensial atom mirip hidrogen diberikan oleh persamaan berikut dengan Z adalah muatan listrik.
V = -Ze2/4πε0r … (2.23)
Bila anda substitusikan persamaan (2.23) ke persamaan (2.22), anda akan mendapatkan persamaan berikut.
∇2Ψ+(8π2m/h2)ï¼»E + (Ze2/4πε0r)ï¼½Ψ = 0 … (2.24)
Ringkasnya, penyelesaian persamaan ini untuk energi atom mirip hidrogen cocok dengan yang didapatkan dari teori Bohr.
BILANGAN KUANTUM
Karena elektron bergerak dalam tiga dimensi, tiga jenis bilangan kuantum (Bab 2.3(b)), bilangan kuantum utama, azimut, dan magnetik diperlukan untuk mengungkapkan fungsi gelombang. Dalam Tabel 2.3, notasi dan nilai-nilai yang diizinkan untuk masing-masing bilangan kuantum dirangkumkan. Bilangan kuantum ke-empat, bilangan kuantum magnetik spin berkaitan dengan momentum sudut elektron yang disebabkan oleh gerak spinnya yang terkuantisasi. Komponen aksial momentum sudut yang diizinkan hanya dua nilai, +1/2(h/2π) dan -1/2(h/2π). Bilangan kuantum magnetik spin berkaitan dengan nilai ini (ms = +1/2 atau -1/2). Hanya bilangan kuantum spin sajalah yang nilainya tidak bulat.
Tabel 2.3 Bilangan kuantum
| Nama (bilangan kuantum) | simbol | Nilai yang diizinkan |
| Utama | n | 1, 2, 3,… |
| Azimut | l | 0, 1, 2, 3, …n – 1 |
| Magnetik | m(ml) | 0, ±1, ±2,…±l |
| Magnetik spin | ms | +1/2, -1/2 |
Simbol lain seperti yang diberikan di Tabel 2.4 justru yang umumnya digunakan. Energi atom hidroegn atau atom mirip hidrogen ditentukan hanya oleh bilangan kuantum utama dan persamaan yang mengungkapkan energinya identik dengan yang telah diturunkan dari teori Bohr.
Tabel 2.4 Simbol bilangan kuantum azimut
| nilai | 0 | 1 | 2 | 3 | 4 |
| simbol | s | p | d | f | g |
d. Orbital
Fungsi gelombang elektron disebut dengan orbital. Bila bilangan koantum utama n = 1, hanya ada satu nilai l, yakni 0. Dalam kasus ini hanya ada satu orbital, dan kumpulan bilangan kuantum untuk orbital ini adalah (n = 1, l = 0). Bila n = 2, ada dua nilai l, 0 dan 1, yang diizinkan. Dalam kasus ada empat orbital yang didefinisikan oelh kumpulan bilangan kuantum: (n = 2, l = 0), (n = 2, l = 1, m = -1), (n = 2, l = 1, m = 0), (n = 2, l = 1, m = +1).
Latihan 2.9 Jumlah orbital yang mungkin.
Berapa banyak orbital yang mungkin bila n = 3. Tunjukkan kumpulan bilangan kuantumnya sebagaimana yang telah dilakukan di atas.
Jawab: Penghitungan yang sama dimungkinkan untuk kumpulan ini (n = 3, l = 0) dan (n = 3, l = 1). Selain itu, ada lima orbital yang betkaitan dengan (n =3, l =2). Jadi, (n = 3, l = 0), (n = 3, l = 1, m = -1), (n =3, l = 1, m =0), (n =3, l = 1, m = +1) � (n =3, l =2, m = -2), (n =3, l = 2, m = -1), (n = 3, l = 2, m = 0), (n = 3, l = 2,m =+1), (n = 3, l = 2, m = +2). Semuanya ada 9 orbital.
Singkatan untuk mendeskripsikan orbita dengan menggunakan bilangan kuantum utama dan simbol yang ada dalam Tabel 2.4 digunakan secara luas. Misalnya orbital dengan kumpulan bilangan kuantum (n = 1, l = 0) ditandai dengan 1s, dan orbital dengan kumpulan bilangan kuantum (n = 2, l = 1) ditandai dengan 2p tidak peduli nilai m-nya.
Sukar untuk mengungkapkan Ψ secara visual karena besaran ini adalah rumus matematis. Namun, Ψ2 menyatakan kebolehjadian menemukan elektron dalam jarak tertentu dari inti. Bila kebolhejadian yang didapatkan diplotkan, anda akan mendapatkan Gambar 2.5. Gambar sferis ini disebut dengan awan elektron.

Bila kita batasi kebolehjadian sehingga katakan kebolehjadian menemukan elektron di dalam batas katakan 95% tingkat kepercayaan, kita dapat kira-kira memvisualisasikan sebagai yang ditunjukkan dalam Gambar 2.6.

KONFIGURASI ELEKTRON ATOM
Bila atom mengnadung lebih dari dua elektron, interaksi antar elektron harus dipertimbangkan, dan sukar untuk menyelesaikan persamaan gelombang dari sistem yang sangat rumit ini. Bila diasumsikan setiap elektron dalam atom poli-elektron akan bergerak dalam medan listrik simetrik yang kira-kira simetrik orbital untuk masing-masing elektron dapat didefinisikan dengan tiga bilangan kuantum n, l dan m serta bilangan kunatum spin ms, seperti dalam kasus atom mirip hidrogen.
Energi atom mirip hidrogen ditentukan hanya oleh bilangan kuantum utama n, tetapi untuk atom poli-elektron terutama ditentukan oleh n dan l. Bila atom memiliki bilangan kuantum n yang sama, semakin besar l, semakin tinggi energinya.
PRINSIP EKSKLUSI PAULI
Menurut prinsip eksklusi Pauli, hanya satu elektron dalam atom yang diizinkan menempati keadaan yang didefinisikan oleh kumpulan tertentu 4 bilangan kuantum, atau, paling banyak dua elektron dapat menempati satu orbital yang didefinisikan oelh tiga bilangan kuantum n, l dan m. Kedua elektron itu harus memiliki nilai ms yang berbeda, dengan kata lain spinnya antiparalel, dan pasangan elektron seperti ini disebut dengan pasangan elektron.
Kelompok elektron dengan nilai n yang sama disebut dengan kulit atau kulit elektron. Notasi yang digunakan untuk kulit elektron diberikan di Tabel 2.5.
Tabel 2.5 Simbol kulit elektron.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| simbol | K | L | M | N | O | P | Q |
Tabel 2.6 merangkumkan jumlah maksimum elektron dalam tiap kulit, mulai kulit K sampai N. Bila atom dalam keadaan paling stabilnya, keadaan dasar, elektron-elektronnya akan menempati orbital dengan energi terendah, mengikuti prinsip Pauli.
Tabel 2.6 Jumlah maksimum elektron yang menempati tiap kulit.
| n | kulit | l | simbol | Jumlah maks elektron | total di kulit | |
| 1 | K | 0 | 1s | 2 | (2 = 2×12) | |
| 2 | L | 0 | 2s | 2 | (8 = 2×22) | |
| 1 | 2p | 6 | ||||
| 3 | M | 0 | 3s | 2 | (18 = 2×32) | |
| 1 | 3p | 6 | ||||
| 2 | 3d | 10 | ||||
| 4 | N | 0 | 4s | 2 | (32 = 2×42) | |
| 1 | 4p | 6 | ||||
| 2 | 4d | 10 | ||||
| 3 | 4f | 14 | ||||
Di Gambar 2.7, tingkat energi setiap orbital ditunjukkan. Dengan semakin tingginya energi orbital perbedaan energi antar orbital menjadi lebih kecil, dan kadang urutannya menjadi terbalik. Konfigurasi elektron setiap atom dalam keadaan dasar ditunjukkan dalam Tabel 5.4. Konfigurasi elektron kulit terluar dengan jelas berubah ketika nomor atomnya berubah. Inilah teori dasar hukum periodik, yang akan didiskusikan di Bab 5.
Harus ditambahkan di sini, dengan menggunakan simbol yang diberikan di Tabel 2.6, konfigurasi elektron atom dapat dungkapkan. Misalnya, atom hidrogen dalam keadaan dasar memiliki satu elektron diu kulit K dan konfigurasi elektronnya (1s1). Atom karbon memiliki 2 elektron di kulit K dan 4 elektron di kulit L. Konfigurasi elektronnya adalah (1s22s22p2).

Eksperimen penemuan
- Eksperimen celah-ganda Thomas Young membuktikan sifat gelombang dari cahaya. (sekitar 1805)
- Henri Becquerel menemukan radioaktivitas (1896)
- Joseph John Thomson - eksperimen tabung sinar kathoda (menemukan elektron dan muatan negatifnya) (1897)
- Penelitian radiasi benda hitam antara 1850 dan 1900, yang tidak dapat dijelaskan tanpa konsep kuantum.
- Robert Millikan - eksperimen tetesan oli, membuktikan bahwa muatan listrik terjadi dalam kuanta (seluruh unit), (1909)
- Ernest Rutherford - eksperimen lembaran emas menggagalkan model puding plum atom yang menyarankan bahwa muatan positif dan masa atom tersebar dengan rata. (1911)
- Otto Stern dan Walter Gerlach melakukan eksperimen Stern-Gerlach, yang menunjukkan sifat kuantisasi partikel spin (1920)
- Clyde L. Cowan dan Frederick Reines meyakinkan keberadaan neutrino dalam eksperimen neutrino (1955)
Bukti dari mekanika kuantum
Mekanika kuantum sangat berguna untuk menjelaskan perilaku atom dan partikel subatomik seperti proton, neutron dan elektron yang tidak mematuhi hukum-hukum fisika klasik. Atom biasanya digambarkan sebagai sebuah sistem di mana elektron (yang bermuatan listrik negatif) beredar seputar nukleus atom (yang bermuatan listrik positif). Menurut mekanika kuantum, ketika sebuah elektron berpindah dari tingkat energi yang lebih tinggi (misalnya dari n=2 atau kulit atom ke-2 ) ke tingkat energi yang lebih rendah (misalnya n=1 atau kulit atom tingkat ke-1), energi berupa sebuah partikel cahaya yang disebut foton, dilepaskan. Energi yang dilepaskan dapat dirumuskan sbb:
keterangan:
Dalam spektrometer massa, telah dibuktikan bahwa garis-garis spektrum dari atom yang di-ionisasi tidak kontinyu, hanya pada frekuensi/panjang gelombang tertentu garis-garis spektrum dapat dilihat. Ini adalah salah satu bukti dari teori mekanika kuantum.
Peradaban manusia minimal mengenal tiga jenis mekanika, yaitu:
Mekanika Newtonian - dikembangkan Newton berdasarkan data percobaan dan pemikiran Galileo Galilei tentang gerak benda, pemikiran Copernicus tentang gerak revolusi planet-planet terhadap matahari (selanjutnya dikembangkan Keppler menjadi tiga hukumnya mengenai gerak planet mengelilingi matahari), dan data perbintangan Thyco Brahe (Newton melakukan kecurangan dengan mencuri data ini tanpa persetujuan pihak Thyco Brahe).
Mekanika Relativistik - dikembangkan oleh Einstein lewat Teori Relativitas Khusus dan Umum, terutama berdasarkan Relativitas Khusus. Intinya besaran-besaran fisis seperti waktu, panjang, dan massa adalah besaran relatif tergantung kecepatan pengamat dan yang diamati (tentu pengecualian ditujukan untuk kecepatan cahaya yang konstan tak tergantung pengamat)
Mekanika Kuantum - dikembangkan oleh kumpulan ilmuwan paling cemerlang abad dua puluh (dimulai akhir abad 19) seperti Schrodinger, Planck, Heisenberg, Bohr, dan Broglie (ada kemungkinan Einstein ikut mengembangkannya dengan mengajukan tantangan-tantangan yang harus dijawab oleh mekanika kuantum). Mekanika Kuantum adalah proyek fisika teoretis paling ambisius dengan tujuan akhir menggabungkan semua hukum fisika dalam satu teori tunggal. (General Unified Theory - Theory of Everything).
Apa yang dikatakan mekanika kuantum tentang ruang-waktu ? Mekanika Kuantum adalah sebuah teori ajaib sepanjang masa (mungkin sebentar lagi rekornya akan diambil alih oleh Wolfram dengan teori digital universenya). Mekanika Kuantum menyatakan
1. Tak ada realitas selama hal itu belum diukur.
2. Tidak ada pengukuran yang dapat menghasilkan nilai yang pasti karena hukum fisika melarang hal ini. Heisenberg merumuskannya dengan elegan dalam asas ketidakpastian Heisenberg.
4. Linguistik manusia telah menipu manusia dalam mempelajari hukum alam. Definisi tentang partikel, gelombang, massa, dan energi misalnya ternyata bukanlah besaran fisis sebenarnya melainkan hanyalah kamuflase fisis. Broglie menyatakan partikel dapat dipandang sebagai gelombang tergantung momentumnya (namun hal sebaliknya belum tentu benar, kecuali untuk gelombang cahaya yang dapat dipandang sebagai gelombang maupun partikel), Einstein menyatakan massa dapat dipandang sebagai energi dan sebaliknya (E=mc2 - diturunkan dari relativitas khusus). Ini sulit dijelaskan, pokoknya massa dan energi adalah kamuflase terhadap besaran fisis yang lebih fundamental
5. Ada kemungkinan besaran-besaran fisis adalah besaran diskrit bukan kontinu. Pemecahan terhadap fungsi gelombang Schrodinger membolehkan kita memandang alam semesta sebagai parameter ruang-waktu diskrit.
Mekanika klasik adalah bagian dari ilmu fisika mengenai gaya yang bekerja pada benda. Sering dinamakan "mekanika Newton" dari Newton dan hukum gerak Newton. Mekanika klasik dibagi menjadi sub bagian lagi, yaitu statika (mempelajari benda diam), kinematika (mempelajari benda bergerak), dan dinamika (mempelajari benda yang terpengaruh gaya). Lihat juga mekanika.
Mekanika klasik menghasilkan hasil yang sangat akurat dalam kehidupan sehari-hari. Dia diikuti oleh relativitas khusus untuk sistem yang bergerak dengan kecepatan sangat tinggi, mendekati kecepatan cahaya, mekanika kuantum untuk sistem yang sangat kecil, dan medan teori kuantum untuk sistem yang memiliki kedua sifat di atas. Namun, mekanika klasik masih sangat berguna, karena ia lebih sederhana dan mudah diterapkan dari teori lainnya, dan dia juga memiliki perkiraan yang valid dan luas terapannya. Mekanika klasik dapat digunakan untuk menjelaskan gerakan benda sebesar manusia (seperti gasing dan bisbol), juga benda-benda astronomi (seperti planet dan galaksi, dan beberapa benda mikroskopis (seperti molekul organik).
Mekanika klasik menggambarkan dinamika partikel atau sistem partikel. Dinamika partikel demikian, ditunjukkan oleh hukum-hukum Newton tentang gerak, terutama oleh hukum kedua Newton. Hukum ini menyatakan, "Sebuah benda yang memperoleh pengaruh gaya atau interaksi akan bergerak sedemikian rupa sehingga laju perubahan waktu dari momentum sama dengan gaya tersebut".
Hukum-hukum gerak Newton baru memiliki arti fisis, jika hukum-hukum tersebut diacukan terhadap suatu kerangka acuan tertentu, yakni kerangka acuan inersia (suatu kerangka acuan yang bergerak serba sama - tak mengalami percepatan). Prinsip Relativitas Newtonian menyatakan, "Jika hukum-hukum Newton berlaku dalam suatu kerangka acuan maka hukum-hukum tersebut juga berlaku dalam kerangka acuan lain yang bergerak serba sama relatif terhadap kerangka acuan pertama".
Konsep partikel bebas diperkenalkan ketika suatu partikel bebas dari pengaruh gaya atau interaksi dari luar sistem fisis yang ditinjau (idealisasi fakta fisis yang sebenarnya). Gerak partikel terhadap suatu kerangka acuan inersia tak gayut (independen) posisi titik asal sistem koordinat dan tak gayut arah gerak sistem koordinat tersebut dalam ruang. Dikatakan, dalam kerangka acuan inersia, ruang bersifat homogen dan isotropik. Jika partikel bebas bergerak dengan kecepatan konstan dalam suatu sistem koordinat selama interval waktu tertentu tidak mengalami perubahan kecepatan, konsekuensinya adalah waktu bersifat homogen.
1. Prinsip Hamilton
Jika ditinjau gerak partikel yang terkendala pada suatu permukaan bidang, maka diperlukan adanya gaya tertentu yakni gaya konstrain yang berperan mempertahankan kontak antara partikel dengan permukaan bidang. Namun sayang, tak selamanya gaya konstrain yang beraksi terhadap partikel dapat diketahui. Pendekatan Newtonian memerlukan informasi gaya total yang beraksi pada partikel. Gaya total ini merupakan keseluruhan gaya yang beraksi pada partikel, termasuk juga gaya konstrain. Oleh karena itu, jika dalam kondisi khusus terdapat gaya yang tak dapat diketahui, maka pendekatan Newtonian tak berlaku. Sehingga diperlukan pendekatan baru dengan meninjau kuantitas fisis lain yang merupakan karakteristik partikel, misal energi totalnya. Pendekatan ini dilakukan dengan menggunakan prinsip Hamilton, dimana persamaan Lagrange yakni persamaan umum dinamika partikel dapat diturunkan dari prinsip tersebut.
Prinsip Hamilton mengatakan, "Dari seluruh lintasan yang mungkin bagi sistem dinamis untuk berpindah dari satu titik ke titik lain dalam interval waktu spesifik (konsisten dengan sembarang konstrain), lintasan nyata yang diikuti sistem dinamis adalah lintasan yang meminimumkan integral waktu selisih antara energi kinetik dengan energi potensial.".
2. Persamaan Lagrange
Persamaan gerak partikel yang dinyatakan oleh persamaan Lagrange dapat diperoleh dengan meninjau energi kinetik dan energi potensial partikel tanpa perlu meninjau gaya yang beraksi pada partikel. Energi kinetik partikel dalam koordinat kartesian adalah fungsi dari kecepatan, energi potensial partikel yang bergerak dalam medan gaya konservatif adalah fungsi dari posisi.
Jika didefinisikan Lagrangian sebagai selisih antara energi kinetik dan energi potensial. Dari prinsip Hamilton, dengan mensyaratkan kondisi nilai stasioner maka dapat diturunkan persamaan Lagrange. Persamaan Lagrange merupakan persamaan gerak partikel sebagai fungsi dari koordinat umum, kecepatan umum, dan mungkin waktu. Kegayutan Lagrangian terhadap waktu merupakan konsekuensi dari kegayutan konstrain terhadap waktu atau dikarenakan persamaan transformasi yang menghubungkan koordinat kartesian dan koordinat umum mengandung fungsi waktu. Pada dasarnya, persamaan Lagrange ekivalen dengan persamaan gerak Newton, jika koordinat yang digunakan adalah koordinat kartesian.
3. Mengapa perlu formulasi Lagrangian?
Dalam mekanika Newtonian, konsep gaya diperlukan sebagai kuantitas fisis yang berperan dalam aksi terhadap partikel. Dalam dinamika Lagrangian, kuantitas fisis yang ditinjau adalah energi kinetik dan energi potensial partikel. Keuntungannya, karena energi adalah besaran skalar, maka energi bersifat invarian terhadap transformasi koordinat.
Dalam kondisi tertentu, tidaklah mungkin atau sulit menyatakan seluruh gaya yang beraksi terhadap partikel, maka pendekatan Newtonian menjadi rumit pula atau bahkan tak mungkin dilakukan. Oleh karena itu, pada perkembangan berikutnya dari mekanika, prinsip Hamilton berperan penting karena ia hanya meninjau energi partikel saja [1].
4. Mekanika Klasik dan Fisika Modern
Meskipun mekanika klasik hampir cocok dengan teori "klasik" lainnya seperti elektrodinamika dan termodinamika klasik, ada beberapa ketidaksamaan ditemukan di akhir abad 19 yang hanya bisa diselesaikan dengan fisika modern. Khususnya, elektrodinamika klasik tanpa relativitas memperkirakan bahwa kecepatan cahaya adalah relatif konstan dengan Luminiferous aether, perkiraan yang sulit diselesaikan dengan mekanik klasik dan yang menuju kepada pengembangan relativitas khusus. Ketika digabungkan dengan termodinamika klasik, mekanika klasik menuju ke paradoks Gibbs yang menjelaskan entropi bukan kuantitas yang jelas dan ke penghancuran ultraviolet yang memperkirakan benda hitam mengeluarkan energi yang sangat besar. Usaha untuk menyelesaikan permasalahan ini menuju ke pengembangan mekanika kuantum.
Model Atom Mekanika Kuantum-Model Atom Modern Yang Dipakai Sampai Saat Ini
Salah satu kelemahan model atom Bohr hanya bisa dipakai untuk menjelaskan model atom hydrogen dan atom atau ion yang memiliki konfigurasi elektron seperti atom hydrogen, dan tidak bisa menjelaskan untuk atom yang memiliki banyak elektron.
Werner heinsberg (1901-1976), Louis de Broglie (1892-1987), dan Erwin Schrödinger (1887-1961) merupakan para ilmuwan yang menyumbang berkembangnya model atom modern atau yang disebut sebagai model atom mekanika kuantum.
Pernyataan de Broglie yang menyatakan bahwa partikel dapat bersifat seperti gelombang telah menginspirasi Schrödinger untuk menyusun model atomnya dengan memperhatikan sifat elektron bukan hanya sebagai partikel tapi juga sebagai gelombang, artinya dia menggunakan dualisme sifat elektron.
Menurut Schrödinger elektron yang terikat pada inti atom dapat dianggap memiliki sifat sama seperti “standing wave” , anda bisa membayangkan gelombang standing wave ini seperti senar pada gitar (lihat gambar). Ciri standing wave ini ujung-ujungnya harus memiliki simpul sehingga ½ gelombang yang dihasilkan berjumlah bilangan bulat.

Hal yang sama dapat diterapkan apabila kita menganggap elektron dalam atom hydrogen sebagai “standing wave”. Hanya orbit dengan dengan jumlah ½ gelombang tertentu saja yang diijinkan, orbit dengan jumlah ½ gelombang yang bukan merupakan bilangan bulat tidak diijinkam. Hal inilah penjelasan yang rasional mengapa energi dalam atom hydrogen terkuantisasi. (lihat gambar)

Schrödinger kemudian mengajukan persamaan yang kemudian dikenal dengan nama “persamaan gelombang Schrödinger” yaitu :
H? = E?
? disebut sebagai fungsi gelombang, H adalah satu set intruksi persamaan matematika yang disebut sebagai operator, dan E menunjukan total energi dari atom. Penyelesaian persamaan ini menghasilkan berbagai bentuk penyelesaian dimana setiap penyelesain ini melibatkan fungsi gelombang ? yang dikarakteristikkan oleh sejumlah nilai E. Fungsi gelombang ? yang spesisfik dari penyelesaian persamaan gelombang Schrödinger disebut sebagai “orbital”
Apakah orbital itu? Orbital adalah daerah kebolehjadian kita menemukan elektron dalam suatu atom atau bisa dikatakan daerah dimana kemungkinan besar kita dapat menemukan elektron dalam suatu atom.
Bedakan dengan istilah orbit yang dipakai di model atom Bohr. Orbit berupa lintasan dimana kita bisa tahu lintasan dimana elektron mengelilingi inti, tapi pada orbital kita tidak tahu bagaimana bentuk lintasan elektron yang sedang mengelilingi inti. Yang dapat kita ketahui adalah dibagian mana kemungkinan besar kita dapat menemukan elektron dalam atom.
Werner Heisenberg menjelaskan secara gamblang tentang sifat alami dari orbital, analisis matematika yang dihasilkannya menyatakan bahwa kita tidak bisa secara pasti menentukan posisi serta momentum suatu partikel pada kisaran waktu tertentu. Secara matematis azas ketidakpastian Heisenberg ditulis sebagai berikut:
?x . ?(mv) ? h/4?
?x adalah ketidakpastian menentukan posisi dan ?(mv) adalah ketidakpastian momentum dan h adalah konstanta Plank. Arti persamaan diatas adalah semakin akurat kita menentukan posisi suatu partikel maka semakin tidak akurat nilai momentum yang kita dapatkan, dan sebaliknya.
Pembatasan ini sangat penting bila kita memmpelajari partikel yang sangat kecil seperti elektron, oleh sebab itulah kita tidak bisa menentukan secara pasti posisi elektron yang sedang mengelilingi inti atom seperti yang ditunjukan oleh model atom Bohr, dimana elektron bergerak dalam orbit yang berbentuk lingkaran. Disinilah mulai diterimanya model atom mekanika kuantum yang diajukan oleh Schrödinger.
Sesuai dengan azaz Heisenberg ini maka fungsi gelombang tidak dapat menjelaskan secara detail pergerakan elektron dalam atom, kecuali fungsi gelombang kuadrat (?2) yang dapat diartikan sebagai probabilitas distribusi elektron dalam orbital. Hal ini bisa dipakai unutk menggambarkan bentuk orbital dalam bentuk distribusi elektron, atau dikenal sebagai peta densitas.
Model Atom Mekanika Kuantum
Penjelasan tentang struktur atom yang lebih lengkap diperlukan untuk mengetahui struktur yang lebih detil tentang elektron di dalam atom. Model atom yang lengkap harus dapat menerangkan misteri efek Zeeman dan sesuai untuk atom berelektron banyak. Dua gejala ini tidak dapat diterangkan oleh model atom Bohr.
Efek Zeeman
Spektrum garis atomik teramati saat arus listrik dialirkan melalui gas di dalam sebuah tabung lecutan gas. Garis-garis tambahan dalam spektrum emisi teramati jika atom-atom tereksitasi diletakkan di dalam medan magnet luar. Satu garis di dalam spektrum garis emisi terlihat sebagai tiga garis (dengan dua garis tambahan) di dalam spektrum apabila atom diletakkan di dalam medan magnet. Terpecahnya satu garis menjadi beberapa garis di dalam medan magnet dikenal sebagai efek Zeeman.

pemisahan garis spektrum atomik di dalam medan magnet
Efek Zeeman tidak dapat dijelaskan menggunakan model atom Bohr. Dengan demikian, diperlukan model atom yang lebih lengkap dan lebih umum yang dapat menjelaskan efek Zeeman dan spektrum atom berelektron banyak.
Model Atom Mekanika Kuantum
Sebelumnya kita sudah membahas tentang dualisme gelombang-partikel yang menyatakan bahwa sebuah objek dapat berperilaku baik sebagai gelombang maupun partikel. dalam skala atomik, elektron dapat kita tinjau sebagai gejala gelombang yang tidak memiliki posisi tertentu di dalam ruang. Posisi sebuah elektron diwakili oleh kebolehjadian atau peluang terbesar ditemukannya elektron di dalam ruang.
Demi mendapatkan penjelasan yang lengkap dan umum dari struktur atom, prinsip dualisme gelombang-partikel digunakan. Di sini gerak elektron digambarkan sebagai sebuah gejala gelombang. Persamaan dinamika Newton yang sedianya digunakan untuk menjelaskan gerak elektron digantikan oleh persamaan Schrodinger yang menyatakan fungsi gelombang untuk elektron. Model atom yang didasarkan pada prinsip ini disebut model atom mekanika kuantum.

posisi dan keberadaan elektron di dalam atom dinyatakan sebagai peluang terbesar elektron di dalam atom
Persamaan Schrodinger untuk elektron di dalam atom dapat memberikan solusi yang dapat diterima apabila ditetapkan bilangan bulat untuk tiga parameter yang berbeda yang menghasilkan tiga bilangan kuantum. Ketiga bilangan kuantum ini adalah bilangan kuantum utama, orbital, dan magnetik. Jadi, gambaran elektron di dalam atom diwakili oleh seperangkat bilangan kuantum ini.
Bilangan Kuantum Utama
Dalam model atom Bohr, elektron dikatakan berada di dalam lintasan stasioner dengan tingkat energi tertentu. Tingkat energi ini berkaitan dengan bilangan kuantum utama dari elektron. Bilangan kuantum utama dinyatakan dengan lambang n sebagaimana tingkat energi elektron pada lintasan atau kulit ke-n. untuk atom hidrogen, sebagaimana dalam model atom Bohr, elektron pada kulit ke-n memiliki energi sebesar
![]() Adapun untuk atom berelektron banyak (terdiri atas lebih dari satu elektron), energi elektron pada kulit ke-n adalah
Adapun untuk atom berelektron banyak (terdiri atas lebih dari satu elektron), energi elektron pada kulit ke-n adalah
![]() Dimana Z adalah nomor atom. Nilai-nilai bilangan kuantum utama n adalah bilangan bulat mulai dari 1.
Dimana Z adalah nomor atom. Nilai-nilai bilangan kuantum utama n adalah bilangan bulat mulai dari 1.
n = 1, 2, 3, 4, ….
Bisa dikatakan bahwa bilangan kuantum utama berkaitan dengan kulit elektron di dalam atom. Bilangan kuantum utama membatasi jumlah elektron yang dapat menempati satu lintasan atau kulit berdasarkan persamaan berikut.
Jumlah maksimum elektron pada kulit ke-n adalah 2n2
Bilangan Kuantum Orbital
Elektron yang bergerak mengelilingi inti atom memiliki momentum sudut. Efek Zeeman yang teramati ketika atom berada di dalam medan magnet berkaitan dengan orientasi atau arah momentum sudut dari gerak elektron mengelilingi inti atom. Terpecahnya garis spektum atomik menandakan orientasi momentum sudut elektron yang berbeda ketika elektron berada di dalam medan magnet.
 Tiap orientasi momentum sudut elektron memiliki tingkat energi yang berbeda. Meskipun kecil perbedaan tingkat energi akan teramati apabila atom berada di dalam medan magnet. Momentum sudut elektron dapat dinyatakan sebagai
Tiap orientasi momentum sudut elektron memiliki tingkat energi yang berbeda. Meskipun kecil perbedaan tingkat energi akan teramati apabila atom berada di dalam medan magnet. Momentum sudut elektron dapat dinyatakan sebagai
![]() Dimana
Dimana
![]() Bilangan l disebut bilangan kuantum orbital. Jadi, bilangan kuantum orbital l menentukan besar momentum sudut elektron. Nilai bilangan kuantum orbital l adalah
Bilangan l disebut bilangan kuantum orbital. Jadi, bilangan kuantum orbital l menentukan besar momentum sudut elektron. Nilai bilangan kuantum orbital l adalah
l = 0, 1, 2, 3, … (n – 1)
misalnya, untuk n = 2, nilai l yang diperbolehkan adalah l = 0 dan l = 1.
Bilangan Kuantum Magnetik
Momentum sudut elektron L merupakan sebuah vektor. Jika vektor momentum sudut L diproyeksikan ke arah sumbu yang tegak atau sumbu-z secara tiga dimensi akan didapatkan besar komponen momentum sudut arah sumbu-z dinyatakan sebagai Lz. bilangan bulat yang berkaitan dengan besar Lz adalah m. bilangan ini disebut bilangan kuantum magnetik. Karena besar Lz bergantung pada besar momentum sudut elektron L, maka nilai m juga berkaitan dengan nilai l.
m = −l, … , 0, … , +l
misalnya, untuk nilai l = 1, nilai m yang diperbolehkan adalah −1, 0, +1.
Gambar
Bilangan Kuantum Spin
Bilangan kuantum spin diperlukan untuk menjelaskan efek Zeeman anomali. Anomali ini berupa terpecahnya garis spektrum menjadi lebih banyak garis dibanding yang diperkirakan. Jika efek Zeeman disebabkan oleh adanya medan magnet eksternal, maka efek Zeeman anomali disebabkan oleh rotasi dari elektron pada porosnya. Rotasi atau spin elektron menghasilkan momentum sudut intrinsik elektron. Momentum sudut spin juga mempunyai dua orientasi yang berbeda, yaitu spin atas dan spin bawah. Tiap orientasi spin elektron memiliki energi yang berbeda tipis sehingga terlihat sebagai garis spektrum yang terpisah.

garis spektra atom yang terpisah di dalam medan magnet berasal dari spin elektron
Spin elektron diwakili oleh bilangan kuantum tersendiri yang disebut bilangan kuantum magnetik spin (atau biasa disebut spin saja). Nilai bilangan kuantum spin hanya boleh satu dari dua nilai +½ atau −½. jika ms adalah bilangan kuantum spin, komponen momentum sudut arah sumbu-z dituliskan sebagai
Sz = msћ
Dimana
![]()
Spin ke atas dinyatakan dengan
![]()
Spin ke bawah dinyatakan dengan
![]()
Atom Berelektron Banyak
Model atom mekanika kuantum dapat digunakan untuk menggambarkan struktur atom untuk atom berelektron banyak. Posisi atau keadaan elektron di dalam atom dapat dinyatakan menggunakan seperangkat (empat) bilangan kuantum. Misalnya, elektron dengan bilangan kuantum n = 2, l = 1, m = −1 dan ms = −½ menyatakan sebuah elektron pada kulit L, subkulit p, orbital −1 dengan arah spin ke bawah.


 adalah energi (
adalah energi (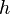 adalah tetapan Planck,
adalah tetapan Planck,  (
( adalah frekuensi dari cahaya (
adalah frekuensi dari cahaya (
Tidak ada komentar:
Posting Komentar